CINEMÁTICA VETORIAL

Cinemática vetorial é a que trata de movimentos levando em conta mais de uma dimensão, com posição, velocidade e aceleração dados em termos de vetores. Num estudo vetorial, a velocidade média de um móvel é um conceito que envolve módulo, direção e sentido. A velocidade vetorial média não mostra o tipo de movimento entre os pontos A e B, nem a trajetória do móvel. É importante lembrar que as grandezas vetoriais exigem valor numérico, unidade de medida, direção e sentido. Nesse contexto também temos os conceitos de deslocamento, velocidade, aceleração e força.

Graficamente, um vetor é representado por um segmento orientado de reta.

Conheça os elementos de um vetor:

·                    Direção – Determinado pela reta suporte (r) do vetor.

·                    Módulo – Determinado pelo comprimento do vetor.

·                    Sentido – Determinado pela orientação do segmento.

OPERAÇÕES COM VETORES

ADIÇÃO

Dados dois vetores u e v , define-se o vetor soma u + v , conforme indicado nas figuras abaixo.

Regra do triângulo

Regra do paralelogramo

SUBTRAÇÃO

Considerando-se a existência do vetor oposto -v , podemos definir a diferença u - v , como sendo igual
à soma u + ( -v ) .

Veja a figura abaixo:

MULTIPLICAÇÃO POR UM ESCALAR

Dado um vetor u e um escalar l Î R, define-se o vetor l .u , que possui a mesma direção de u e sentido coincidente para l > 0 e sentido oposto para l < 0. O módulo do vetor l .u será igual a

 |l |.u .

PRODUTO INTERNO DE VETORES

Dados dois vetores u e v , define-se o produto interno desses vetores como segue:

u . v = u . v . cos b onde u e v são os módulos dos vetores e b o ângulo formado entre eles.

Da definição acima, infere-se imediatamente que:

a) se dois vetores são paralelos, (b = 0º e cos 0º = 1) então o produto interno deles, coincidirá com o produto dos seus módulos.

b) o produto interno de um vetor por ele mesmo, será igual ao quadrado do seu módulo, pois neste caso, 

b = 0º e cos 0º = 1 \ u.u = u.u.1 = u²

c) se dois vetores são perpendiculares, (b = 90º e cos 90º = 0) então o produto interno deles será nulo.

d) o produto interno de dois vetores será sempre um número real.

e) o produto interno de vetores é também conhecido como produto escalar.

CÁLCULO DO PRODUTO INTERNO EM FUNÇÃO DAS COORDENADAS DO VETOR

Sejam os vetores u = (a, b) = a i + b j e v = (c, d) = c i + d j

Vamos multiplicar escalarmente os vetores u e v.

u.v = (a i + b j).(c i + d j) = ac i.i + ad i.j + bc j.i + bd j.j

Lembrando que os versores i e j são perpendiculares e considerando-se as conclusões acima, teremos: 

i.i = j.j = 1 e i.j = j.i = 0

Daí, fazendo as substituições, vem:

u.v = ac . 1 + ad . 0 + bc . 0 + bd . 1 = ac + bd

Então concluímos que o produto interno de dois vetores, é igual à soma dos produtos das componentes correspondentes ou homônimas.

Unindo a conclusão acima, com a definição inicial de produto interno de vetores, chegamos a uma importante fórmula, a saber:

Sejam os vetores: u = (a,b) e v = (c, d)

Já sabemos que: u.v = u.v.cosb = ac + bd

Logo, o ângulo formado pelos vetores, será tal que:

Onde u e v correspondem aos módulos dos vetores e a, b, c, d são as suas coordenadas.

Portanto, para determinar o ângulo formado por dois vetores, basta dividir o produto interno deles, pelo produto dos seus módulos. Achado o coseno, o ângulo estará determinado.

Veremos um exercício de aplicação, no final deste arquivo.

Vamos demonstrar o teorema de Pitágoras, utilizando o conceito de produto interno de vetores.

Seja o triângulo retângulo da figura abaixo:

É óbvio que: w = u + v

Quadrando escalarmente a igualdade vetorial acima, vem:

w² = u² + 2.u.v + v²

Dos itens (b) e (c) acima, concluímos que w² = w² , u² = u² , v² = v² e u.v = 0 (lembre-se que os vetores ue v são perpendiculares).

Assim, substituindo, vem:

w² = u² + 2.0 + v² , ou, finalmente: w² = u² + v² (o quadrado da hipotenusa é igual à soma dos quadrados dos catetos).

Vetor Posição

Imagine um móvel deslocando-se em uma trajetória aleatória, com uma origem O.

Se colocarmos um plano cartesiano situado nesta origem, então poderemos localizar o móvel nesta trajetória por meio de um vetor.

O vetor 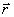é chamado vetor deslocamento e possui módulo, direção e sentido.

=P-O

Velocidade Vetorial

Vetor Velocidade Média: Considere-se um móvel percorrendo a trajetória do gráfico acima, ocupando posições 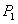 e 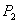 nos instantes 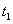e 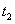, respectivamente.

Sabendo que a velocidade média é igual ao quociente do vetor deslocamento pelo intervalo de tempo:

Observação:

O vetor velocidade média tem a mesma direção e sentido do vetor deslocamento, pois é obtido quando multiplicamos um número positivo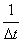 

pelo vetor .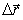

Vetor Velocidade Instantânea: Análogo à velocidade escalar instantânea, quando o intervalo de tempo tender a zero (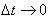), a velocidade calculada será a velocidade instantânea.

então: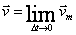 

Aceleração Vetorial

Vetor Aceleração Média: Considerando um móvel que percorre uma trajetória qualquer com velocidade 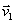em um instante  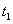e velocidade  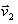em um instante posterior 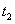, sua aceleração média será dada por:

Observação:

Assim como para o vetor velocidade, o vetor aceleração terá o mesmo sentido e mesma direção do vetor velocidade, pois é resultado do produto deste vetor (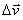) por um número escalar positivo, .

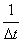Vetor Aceleração Instantânea: A aceleração vetorial instantânea será dada quando o intervalo de tempo tender a zero ().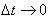

Sabendo esses conceitos, podemos definir as funções de velocidade em função do tempo, deslocamento em função do tempo e a equação de Torricelli para notação vetorial: